Light Attention Vision Modules for Atari
I proposed an attention-based vision policy that can play Atari games based on pixel input. The policy encodes pixels by firstly using convolution layers and then Transformer Encoder, where both the fast attention and regular attention were tested. Experiments comparing vanilla convolutions, fast attention and regular attention on 4 selected Atari games are conducted. I also compare the performance between full encoder layers and simplified layers. The conclusion is that fast attention outperforms regular attention in total reward and simplified encoders outperform full attention-MLP layers in time and total reward under limited experiments.
Introduction
Q-learning algorithm with convolutional neural network, whose input is raw pixels has demonstrated success on several Atari games decades ago (Mnih et al., 2013). The neural network plays the role of both state representation and policy $\pi: \mathcal{S}\rightarrow \mathcal{A}$. Thus, the ability to identify the latent state from raw observations and learn the proper policy from state space to actions are the critical ingredient of the performance of different NN architecture. Transformers (Vaswani et al., 2017) have become SOTA in different areas ranging from natural language processing (NLP), time series prediction, to image generation. The success of Transformers rely on the trainable attention mechanism which identifies complex depencies between elements of each input sequence. Despite the power that attention mechanism processes complex information, attention mechanism is expensive for the fact that it scales quadratically with the length L of the input sequence. Performers ( Choromanski et al., 2020) improve the regular attention with Fast Attention Via positive Orthogonal Random features (FAVOR+) mechanism, which is provably accurate and only takes linear space and time complexity. For this project, I use Deep Q Networks (DQN) with different NN models to train agents directly from raw pixels and compare the performance.
Method
Transformer Encoder
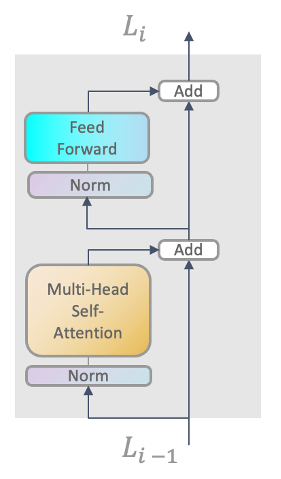
Transformers were proposed originally to process sets instead of sequence since it produces the same output if the input is permuted. To apply Transformers to sequences, a positional encoding is added. Pre-Layer Normalization (Xiong et al., 2020) is used(Figure 1), which is a version of the Transformer that applies Layer Normalization first in each residual block. Pre-LN is more stable for training Transformers, which supports better gradient flow and removes the necessity of a warm-up stage. For the implementation, the Feed Forward block is two fully connected layers with GELU activation. The Feed Forward block introduces much more parameters while the gain is uncertain. Therefore, simplified version of Transformer Encoder with simply attention blocks is tested against the full Transformer Encoder.
FAVOR+ Mechanism
\[\newcommand{\attn}{\mathrm{Attention}} \newcommand{\diag}{\mathrm{diag}}\]Model-free Deep Reinforcement Learning suffers from sample inefficiency. Model requires millions of training steps to learn proper policies from environments. Therefore, models with high complexity could fail to learn policies with limited resources. The canonical Transformer (Vaswani et al., 2017) uses dot-product attention, which takes $ Q,K,V\in \mathbb{R}^{L\times d}$ as input where $L$ is the length of the input sequence and $d$ is the dimension the latent representation. The bidirectional dot-product attention has the form:
\[\begin{align} \attn(Q,K,V) & =D^{-1} AV, \\ A & =\exp(\frac{QK^T}{\sqrt{d}}), \\ D & =\diag(A\mathbf{1}_L). \end{align}\]The time and space complexity are $O(L^2 d)$ and $O(L^2+Ld)$ respectively. FAVOR+ (Choromanski et al., 2020) uses a random feature map \(\phi:\mathbb{R}^d\rightarrow\mathbb{R}_+^r, \forall r>0\) such that the kernel \(K: \mathbb{R}^d\times\mathbb{R}^d\rightarrow\mathbb{R}_+\) has:
\[K(x,y)=\mathbb{E}[ϕ(x)^T ϕ(y)]\]The random feature map $ϕ$ leads to the more efficient attention mechanism:
\[\hat\attn(Q,K,V)=(\hat D^{-1}) (Q' ((K' )^T V))\]Where $\hat{D}=\diag(Q’ ((K’ )^T \mathbf{1}_L ))$. This attention mechanism has time and space complexity $O(Lrd)$ and $O(Lr+Ld+rd)$ respectively (see also Figure 2).
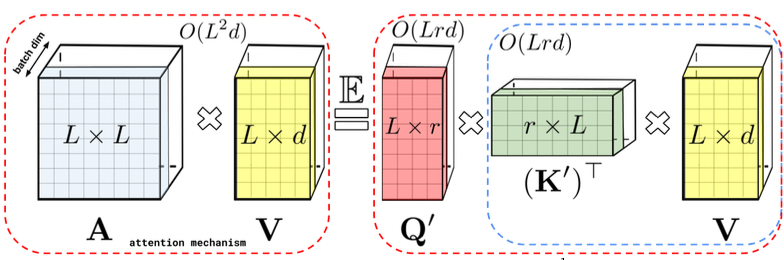
As for experiments, models with regular and fast attention are tested against each other.
Light Attention Vision Module
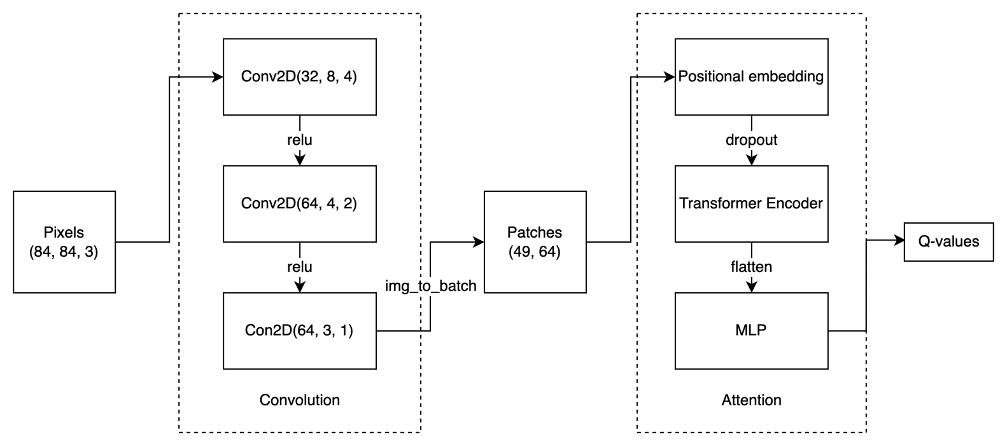
As Figure 3 shows, the Atari games’ pixel observations are firstly resized to $84×84$ pixels and grayscaled. Then 3 consecutive frames are stacked at a new dimension. The stacked frames then become the input of the Convolution module, which consists of 3 sequential Conv2D layers. The feature map after convolutions is of the shape $(H,W,C)$, which is reshaped to $(H×W,C)$ before fed into Transformer Encoder. As for the proposed model, the feature map extracted is of shape $7×7×64$, which is reshape to $49×64$ and passed through one linear layer to obtain sequence of features with embedding size, which is set to 64. The feature embeddings are then added with positional embedding to be fed into Transformer Encoder, which is a sequential of Attention blocks. The processed features from each Attention blocks have same shape as the input features. Here I used multi head self-attention mechanism, the input feature is projected onto each head dimension, which is the feature dimension divided by total number of heads. In the following experiments, the number of heads is 8, the number of layers is 2. The output from Transformer Encoder is flattened and forward through MLP, which contains one hidden layer of size 256 and one linear layer to get estimated Q for each action. Dropout with 0.1 rate is applied in every block.
Experiments and Results
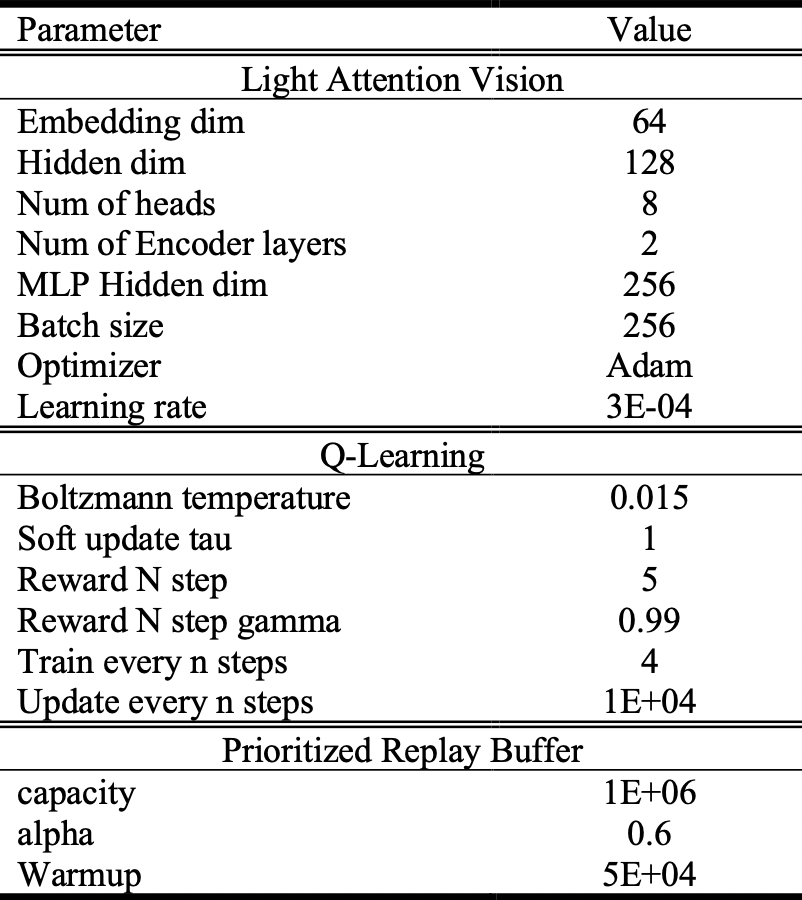
To observe the performance of light attention vision module, experiments on 4 Atari games, which are Breakout, Pong, Asteroids and Tennis, are conducted. Further, to investigate the gain from attention vision module and Feed Forward blocks, vanilla Convolution model and full Transformer Encoder are tested. Moreover, Transformer Encoder with regular dot-product attention mechanism is also tested against fast attention mechanism mentioned before. The same parameters are applied for different models for fair comparision. The parameters are summarized in Table 1. All experiments were conducted on Google Colab with GPU backend and monitored with tensorboard. To better visualize the result, all curves are smoothed by smoothing factor of 0.9.
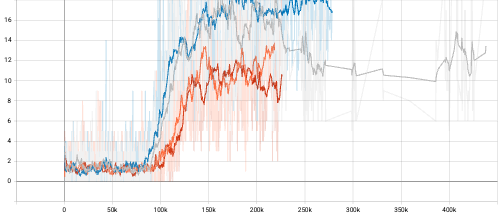
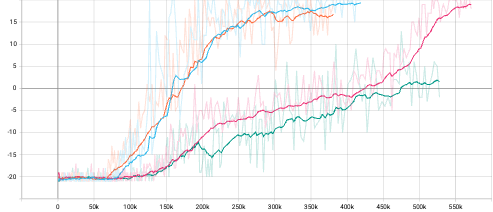
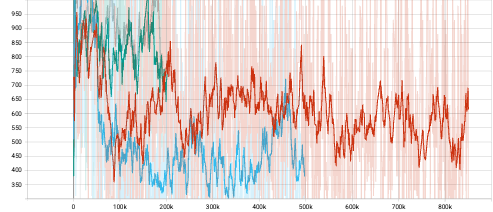
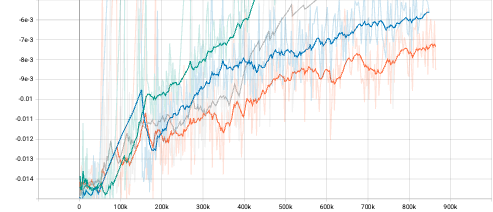
From the episode reward curves the observation is that the light attention vision module performs similarly with vanilla Convolution while being more stable and reaching slightly higher average episode reward but requires longer forward time. The full Transformer Encoder with fast attention and regular attention perform similarly with each other while the fast attention version performs better. And both of the full Encoders need more training steps.
Discussion
When deciding which reinforcement learning algorithm to choose, I first used PPO and it performed well with vanilla Convolution blocks but failed to learn with full Transformer Encoder. I get confused and guessed that my code for light attention vision module contains error so I tried mnist classification to observe if the model is learning from the gradient, and found that the loss drops gradually. Then I tried DQN, which gives better results and starts to learn. The failure of PPO could be resulted from limited trials for hyperparameters and improper value for these parameters, for instance, the capacity of replay buffer. It is also observed that better performance is obtained by using fast attention instead of regular attention. And the MLP block inside the Transformer Encoder layer increases the total trainable parameters while not provides enough performance gains under experiments with limited resources.
For more details, please see the report and code: Report, Code
