TA: Optimization Models and Methods
TA for IEOR E4004. Topics included linear, nonlinear, integer, and dynamic programming.
I served as the Teaching Assistant for Graduate Optimization Models and Methods (IEOR E4004). The course covers linear programming, the simplex method, duality, and nonlinear, integer, and dynamic programming.
My duties included:
- Grading homework and the course project, providing detailed feedback.
- Revising and improving official solutions for assignments.
- Enhancing the final project, “Moving Object Detection,” by creating a more robust and user-friendly coding template.
Final Project Enhancement: Moving Object Detection
I think this is a very interesting project with inspiring questions. The description of this project is as below:
Description
Suppose we would like to extract moving objects from a video. We encode the video as a data matrix \(M ∈ \mathbb{R}^{m×n}\) where each column corresponds to a video frame, and each row corresponds to a pixel. If all the columns are the same, then there is no movement in the video and the data matrix $M$ has rank one. If one or more objects are moving, then they can be can be viewed as noise \(ε ∈ \mathbb{R}^{m×n}\) that is being added to a rank one matrix \(uv^T\) (the fixed background) for some \(u ∈ \mathbb{R}^m\) and \(v ∈ \mathbb{R}^n\). In other words, we have \(M = uv^T + ε\). One can thus try to recover the background (and hence the moving objects) by finding a closest rank one matrix \(xy^T\) to the data matrix $M$, as follows:
\[\inf_{(x,y)\in\mathbb{R}^m\times\mathbb{R}^n}\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^n(x_iy_j-M_{ij})^2\]Selected Questions
- Notice that we do not assume that all the elements of the vector $v$ are equal to one another. What is the benefit of allowing them to be different from one another?
- Determine the update rule of the stochastic gradient descent method applied to the objective function.
- Is the objective function convex? Show that all local minima are global minima when \(ε = 0\). Comment on the empirical success of the approach.
Enhancements for the coding part
I have noticed that some students are having trouble with the current code template, for instance, some students correctly derived the SGD update rule while left the block empty where they are supposed to implement the SGD method.
And when I was trying to do the project, I noticed that some operations require a lot of RAM, and the generated video files are larger than the original video, which could be an issue if the students only have limited storage.
Therefore, I have created a colab version template(LionMail required) for the project that can be viewed by LionMail. Students can make a copy of the colab notebook and implement the algorithm. The features are listed below:
Features:
- Colab notebook
- Colab solves the environment issues, and provides enough storage space
-
SGDfunction for students to implement- The function is put at the beginning of the notebook, so that students could easily figure out what they are supposed to implement
- Supports directly load video from Youtube
- It might be easier to have the option to load the video of interest from Youtube
- A simple moving circle video is provided by default
- I have uploaded a 3s moving circle video, students can use this video to test their implementation before applying the algorithm to larger video
- Clearer hypermarameters

- Colab supports form field, which could be clearer for defining hyper parameters
- Use
numpyfor batch update, instead offor loop- The optimization time could be greatly reduced if the
batch_sizeis large. Below is a comparison ofnumpymethod andfor loopmethod withbatch_size=32 -
numpy: 1min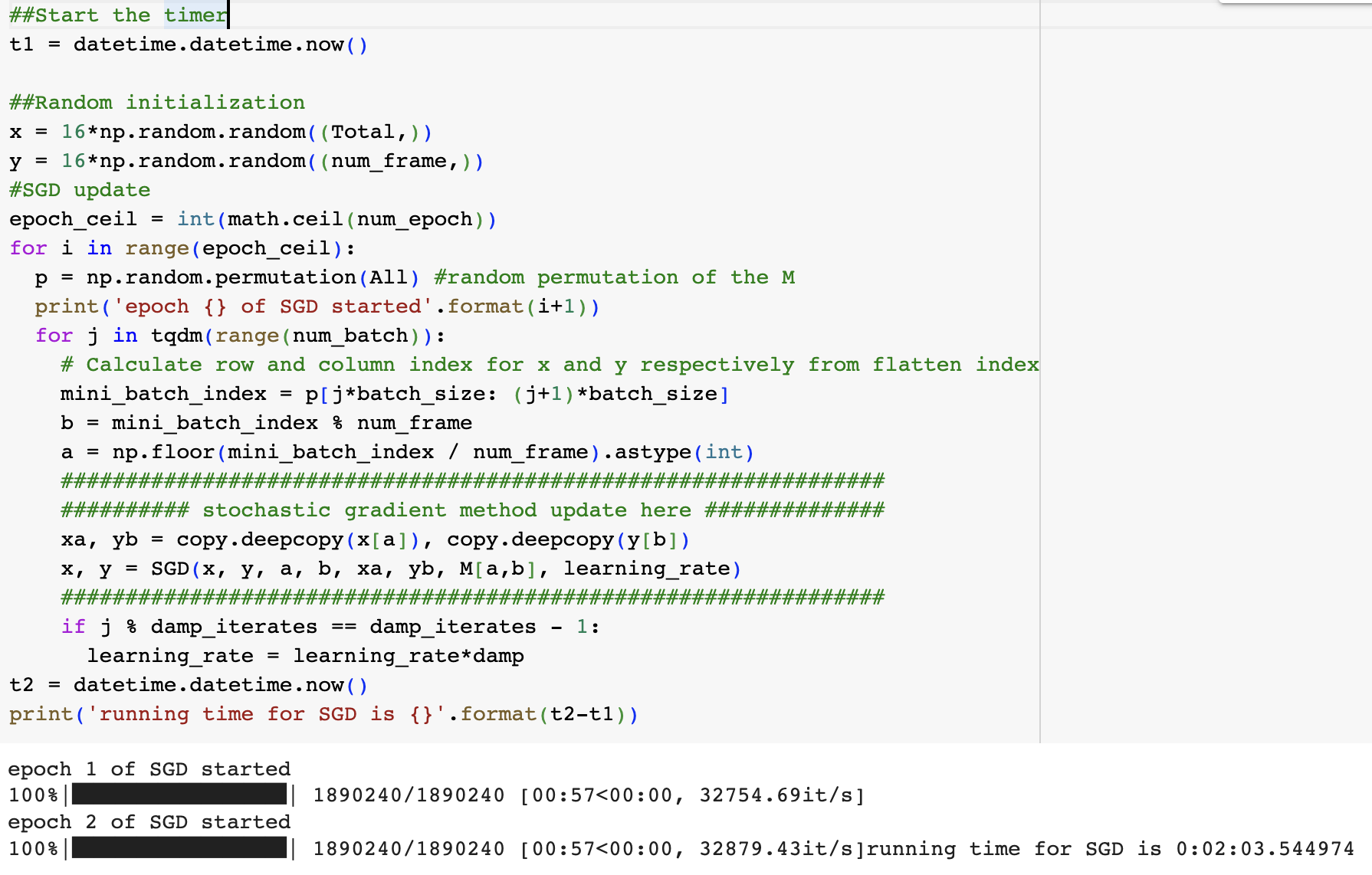
-
for loop: 13min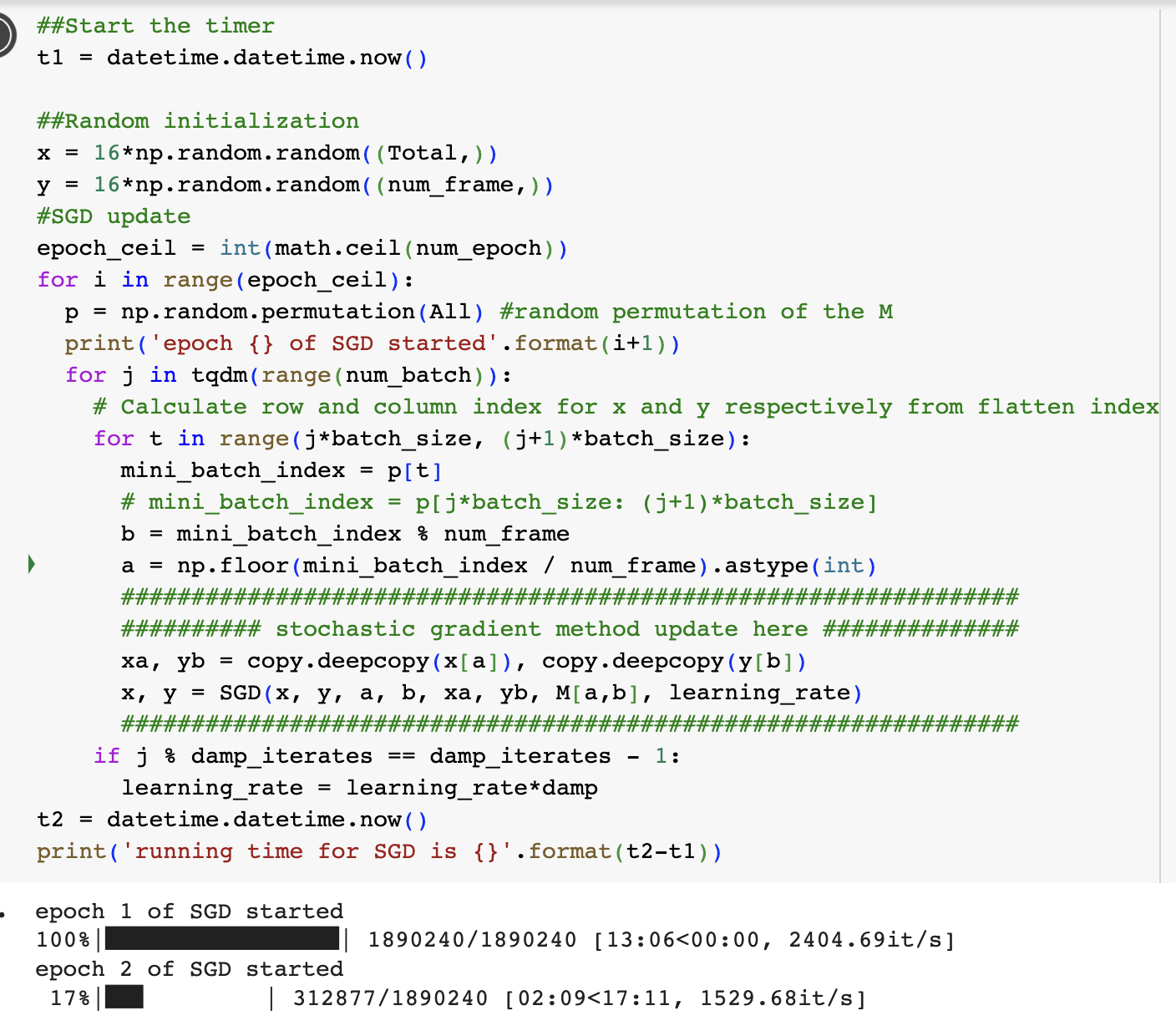
- The optimization time could be greatly reduced if the
- Convert type
float64touint8before $xy^T$ to prevent out-of-memory- For the video of 56Kb (simple moving circle), the
uint8numpy.ndarrayis ~60Mb,float64is ~480Mb. It could easily run out og memory if not converting type before the multiplication.
- The quality of the result video is similar:
- convert to
uint8before multiplication: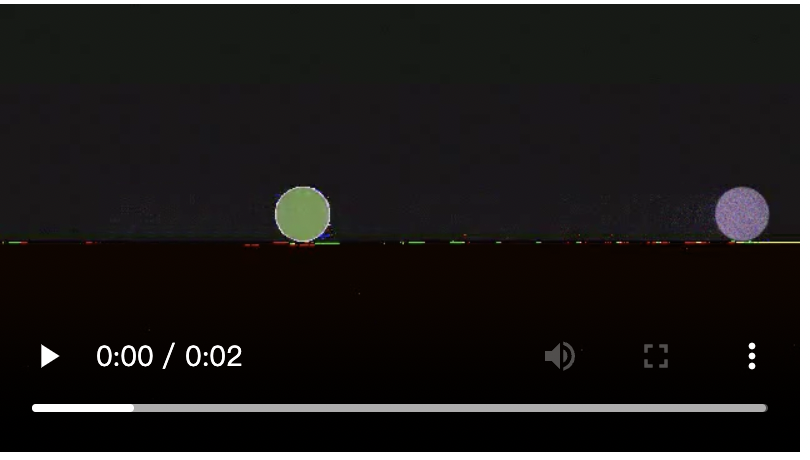
- convert to
uint8after multiplication:
- convert to
- For the video of 56Kb (simple moving circle), the
- Changed variable name
L,Stoestimate_backgroundandnoise - Used
ffmpegto reduce the size of output video- The result video files are much larger than the input video. For instance, the 56Kb video would result in a
background.mp4of size ~750Kb, and amoving_object.mp4of size ~4.6Mb. While usingffmpegcould reduce the size to ~160Kb and ~830Kb, respectively.
- The result video files are much larger than the input video. For instance, the 56Kb video would result in a
- Added an embedded video display feature
- It could be easier for students to display and check their result video on Colab
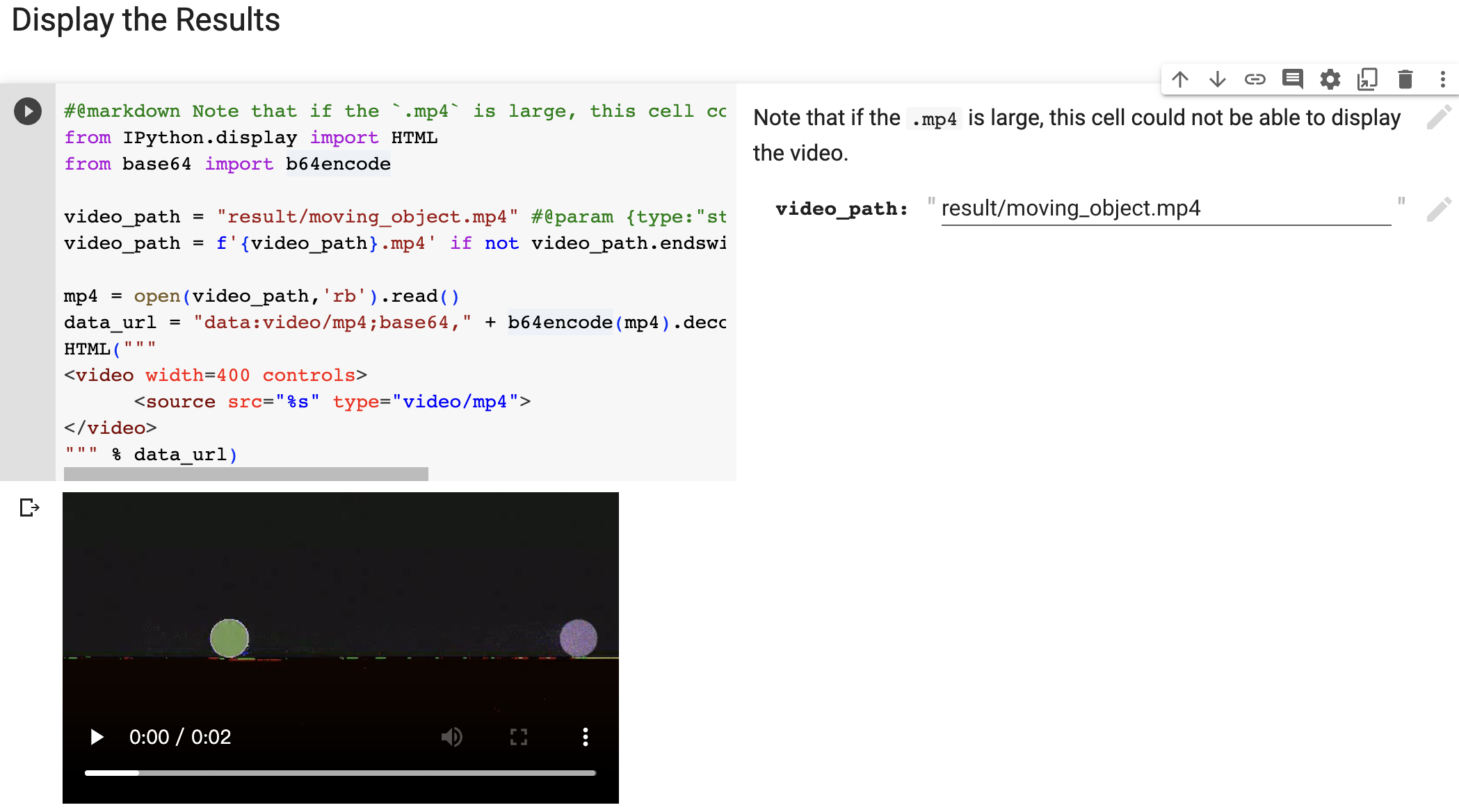
Limitations:
- Video larger than RAM
- The whole video is read in RAM for subsequent operations, so if the video is larger than RAM, the session will be crashed
- Large result video
- Large result video is not able to be displayed by current embedded video display feature, the students might have to download the video and check, which could consume longer time since the download speed of Colab is not fast.