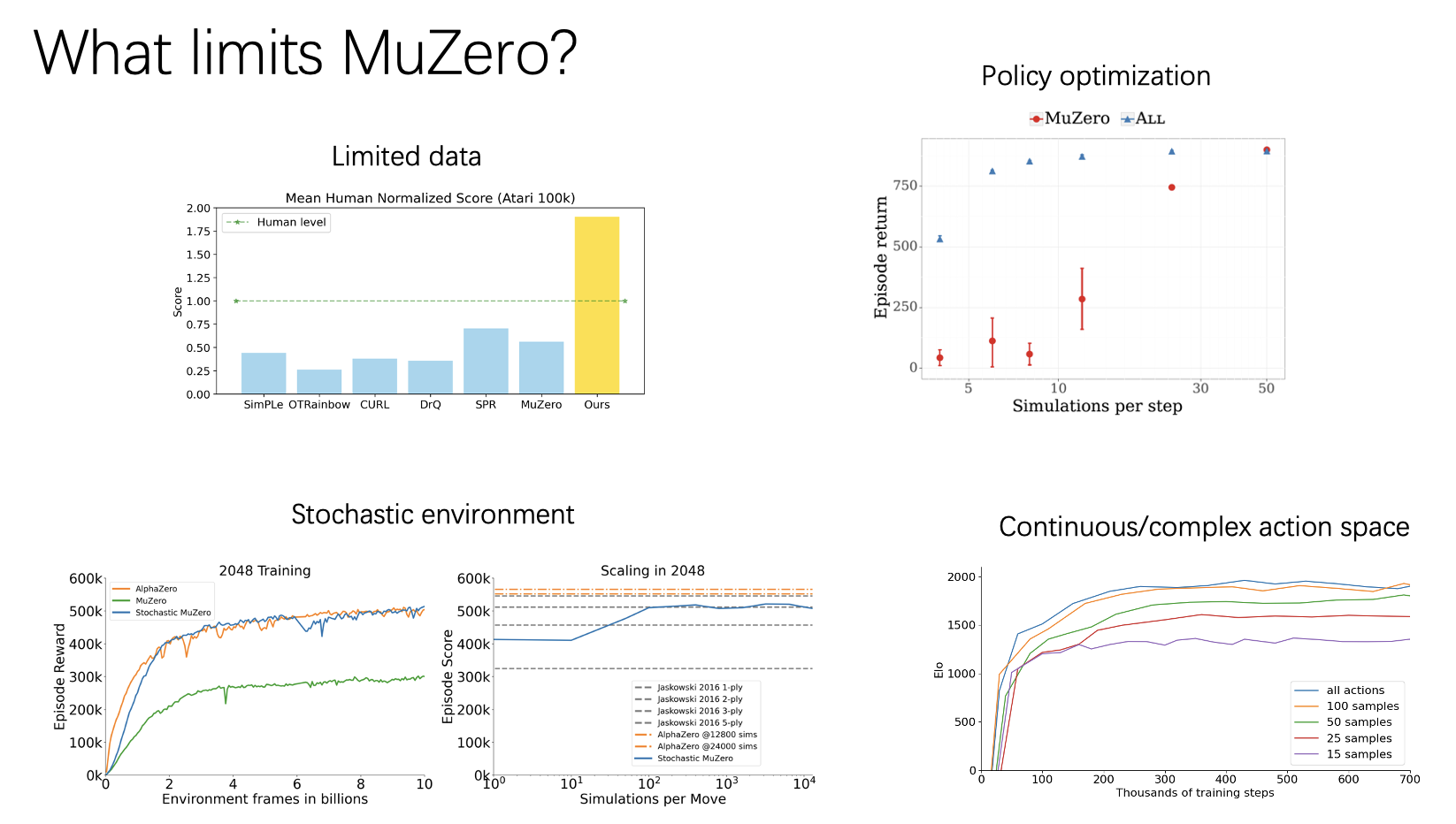
I have found 4 interesting papers that discover and address the limitations of MuZero. EfficientZero and MCTS as regularized policy optimization improve the algorithm itself; SampledMuZero and StochasticMuZero extend the algorithm into a new setting that the original algorithm is not able to perform well.

EfficientZeroLink

The author finds that in limited-data setting, for instance, Atari 100K, which is 2 hours of real-time game experience, MuZero is not that impressive in performance. This leads the author to observe 3 issues.

1. Lack of supervision on environment model. In previous MCTS RL algorithms, the environment model is either given or only trained with rewards, values, and policies, which cannot provide sufficient training signals due to their scalar nature. The problem is more severe when the reward is sparse or the bootstrapped value is not accurate. The MCTS policy improvement operator heavily relies on the environment model. Thus, it is vital to have an accurate one.
2. Predicting the reward from a state is a hard problem. If we only see the first observation, along with future actions, it is very hard both for an agent and a human to predict at which exact future timestep the player would lose a point. However, it is easy to predict the agent will miss the ball after a sufficient number of timesteps if he does not move. In practice, a human will never try to predict the exact step that he loses the point but will imagine over a longer horizon and thus get a more confident prediction.
3. This value target suffers from off-policy issues, since the trajectory is rolled out using an older policy, and thus the value target is no longer accurate. When data is limited, we have to reuse the data sampled from a much older policy, thus exaggerating the inaccurate value target issue.

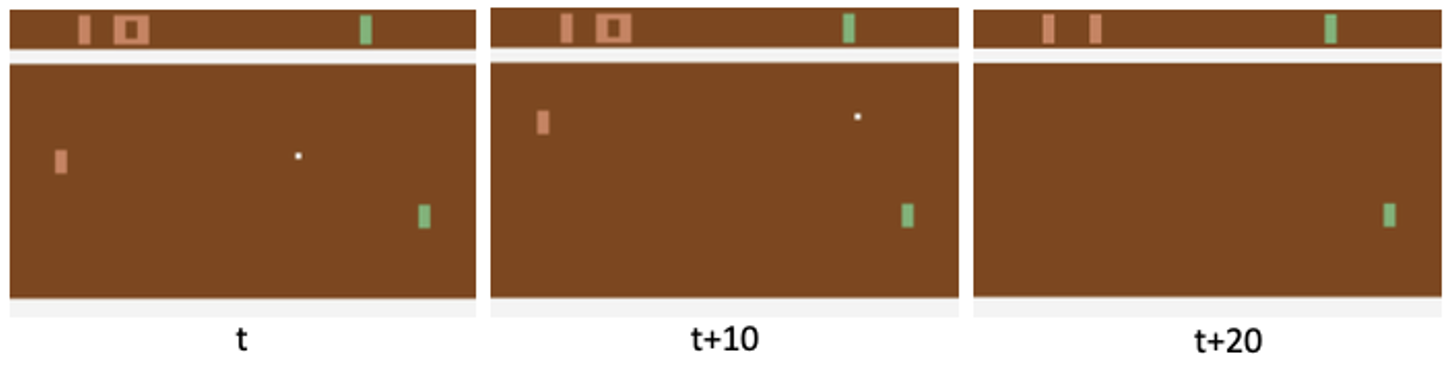
Then 3 methods are proposed to solve each of the issues.

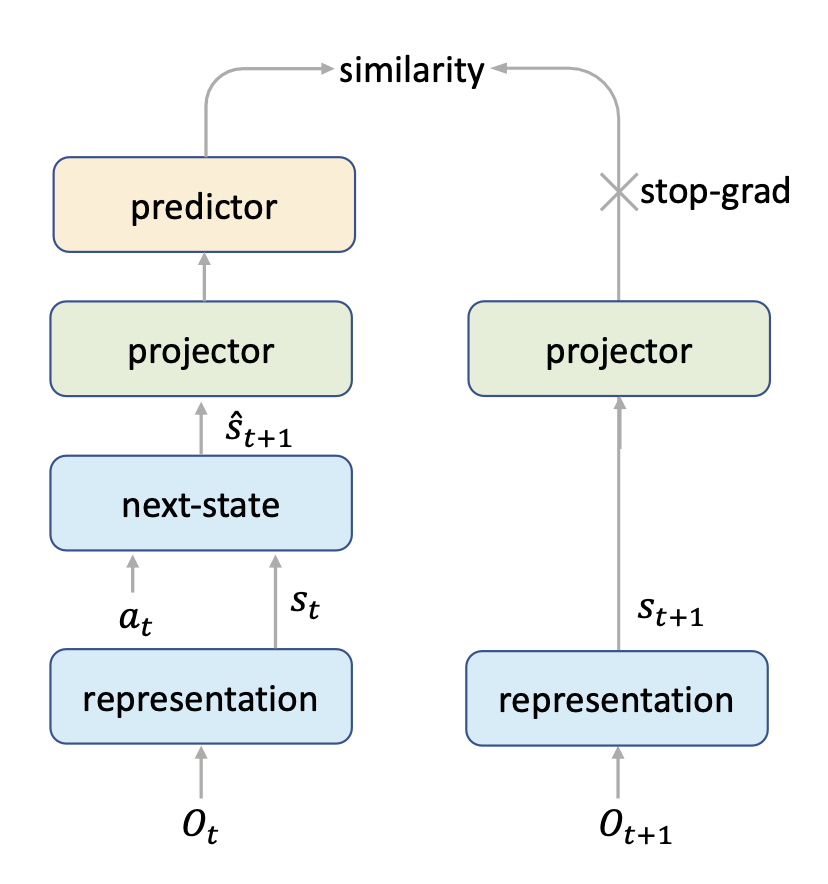
The first one is self-supervised to provide more information. The idea is illustrated by the Figure 2. That is, the hidden state from dynamic function should be similar to the hidden state from the representation of the next observation.

The second is to predict value prefix, which is discounted sum of rewards, instead of stepwise reward. The author chose the LSTM for value prefix prediction. During the training time, the LSTM is supervised at every time step, since the value prefix can be computed whenever a new state comes in. This per-step rich supervision allows the LSTM can be trained well even with limited data.

The third is to re-run MCTS for an adjusted TD steps based on the age of the trajectory. the value target is computed by sampling a trajectory from the replay buffer and computing: \(z_t=\sum_{i=0}^{k-1}\gamma^i u_{t+i}+\gamma^k v_{t+k}\) This value target suffers from off-policy issues, since the trajectory is rolled out using an older policy, and thus the value target is no longer accurate. The author proposed to use rewards of a dynamic horizon $l$ from the old trajectory, where $l<k$ and $l$ should be smaller if the trajectory is older.

MCTS as regularized policy optimizationLink

This paper focuses on policy improvement, and proposed a new method to act, search and update for AlphaZero.

They started from policy optimization, which aims at finding a globally optimal policy $\pi_\theta$, generally using iterative updates. Each updates the current policy $\pi_\theta$ by solving a local maximization problem of the form \(\pi_{\theta'}≜\arg\max_{\textbf{y}\in \mathcal{S}}\mathcal{Q}^T_{\pi_\theta}\textbf{y}-\mathcal{R}(\textbf{y}, \pi_\theta)\), several model-free algorithms employ such policy optimization, for instance, TRPO and MPO set $\mathcal{R}$ to be the KL-divergence between consecutive policies. With idea from policy optimization, they proposed a new policy for AlphaZero: \(\newcommand{\kl}{\mathrm{KL}} \bar{\pi}\triangleq\arg\max_{\textbf{y}\in \mathcal{S}}[\textbf{q}^T\textbf{y}-\lambda_N\kl[\pi_\theta,\textbf{y}] ]\), which in practical can be computed as: \(\bar{\pi}=λ_N\frac{\pi_θ}{α-\textbf{q}}\), where $\alpha$ is used to make $\bar{\pi}$ a proper probability vector and is found through dichotomic search over $(\alpha_{min},\alpha_{max})$, whose value is defined as: \(\alpha_{min}≜\max_{b\in \mathcal{A}}(q[b]+\lambda_N·\pi_\theta[b]), α_{max}≜\max_{b\in\mathcal{A}}q[b]+\lambda_N\).

Then they argued that the empirical visit count distribution $\hat{\pi}$: \(\hat{\pi}(a\mid x)≜\frac{1+n(x,a)}{\mid \mathcal{A}\mid \sum_bn(x,b)}\), has several shortcomings. The first is the efficiency. When a promising new (high-value) leaf is discovered, many additional simulations might be needed before this information is reflected in $\hat{\pi}$; since $\bar{\pi}$ is directly computed from Q-values, this information is updated instantly. The second is the expressiveness. $\hat{\pi}$ is simply the ratio of two integers, and thus has limited expressiveness when the simulation budget is low. The third is that the prior $\pi_\theta$ is trained against the target $\hat{\pi}$, but the latter is only improved for actions that have been sampled at least once during search. This may be problematic for certain actions that would require a large simulation budget to be sampled even once.

The new policy is applied for acting, searching and learning process of AlphaZero.

1. ACT: AlphaZero acts in the real environment by sampling actions according to \(a ∼ \hat{π}(·\ x_{root})\). Instead, they proposed to sample actions sampling according to \(a ∼ \bar{π}(·\mid x_{root})\).
2. SEARCH: During search, they proposed to stochastically sample actions according to $\bar{\pi}$ instead of the deterministic action selection rule. At each node x in the tree, $\bar{π}(·)$ is computed with Q-values and total visit counts at the node.
3. LEARN: AlphaZero computes locally improved policy with tree search and distills such improved policy into $π_θ$. They proposed to use $\bar{π}$ as the target policy in place of $\hat{π}$ to train prior policy

Stochastic MuZeroLink

This paper proposed a method to generalize MuZero to learn and plan in stochastic environment. The idea is to factorize the stochastic state transitions into two deterministic transitions, the first is action $a_t$ conditioned transition from state $s_t$ to afterstate $as_t$(the hypothetical state after the action is applied but before the environment transitions to the next state), the second is a stochastic transition from $as_t$ to the next state $s_{t+1}$ guided by a chance outcome $c_t^i$.

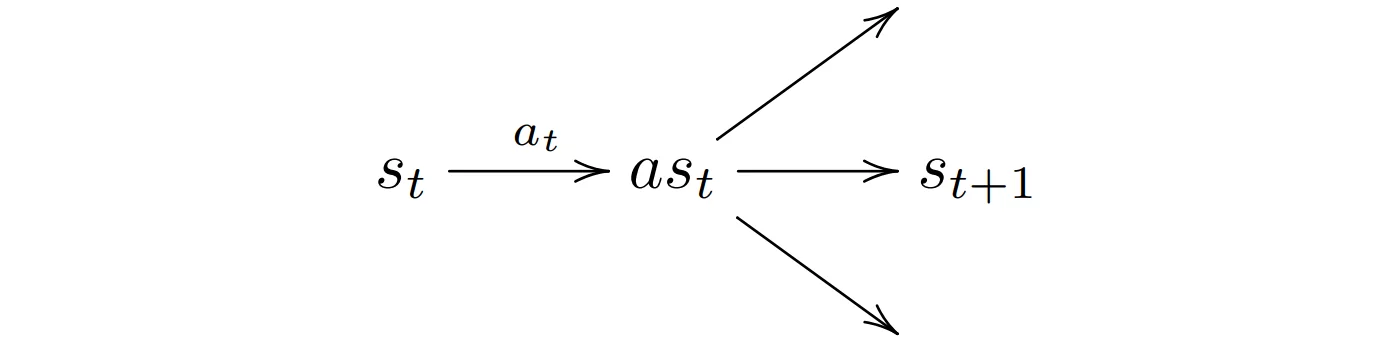
The proposed method applies modifications to planning and learning phases of MuZero. Figure 3 shows the search of Stochastic MuZero, where diamond nodes represent chance nodes and circular nodes represent decision nodes. Edges are selected by applying the pUCT formula in the case of decision nodes, and by sampling the prior $σ$ in the case of chance nodes.

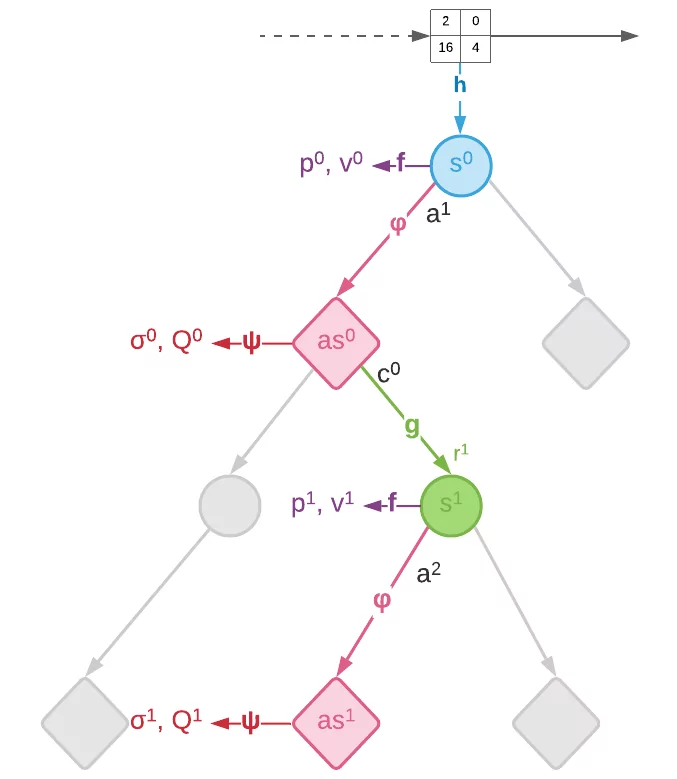
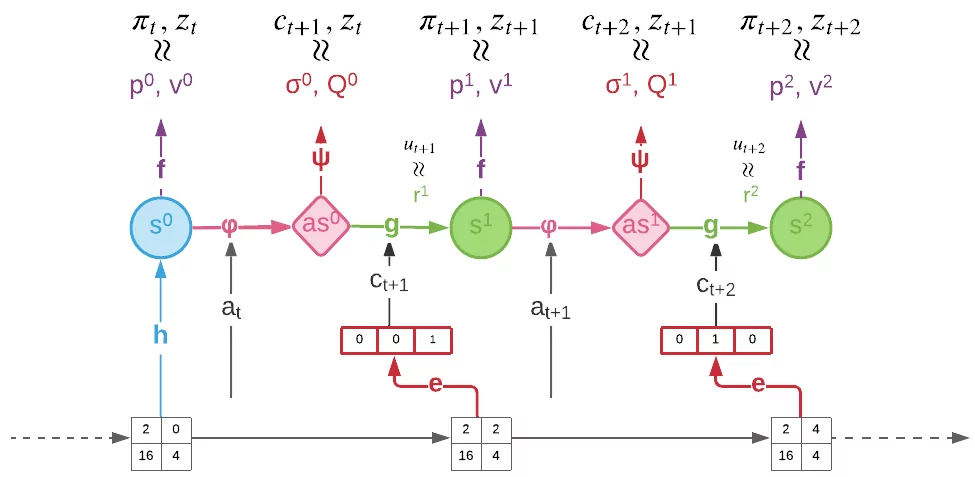
Figure 4 demonstrates the training process of Stochastic MuZero. During the unroll, the encoder $e$ receives the observation as input and generates a chance code $c_{t+k}$ deterministically. The policy, value and reward are trained towards the target \(\pi_{t+k}, z_{t+k}, u_{t+k}\) as MuZero does. The distribution $\sigma_k$ over future codes are trained to predict the code produced by the encoder.

The loss is given by the MuZero loss and a chance loss:

During inference, given the initial observation \(o_{≤t}\) and actions \(a_{t:t+K}\), trajectories from the model can be generated recurrently by unrolling it and by sampling chance outcomes from the distribution \(c_{t+k+1}∼σ_t^k\).

Sampled MuZeroLink

This paper focuses on the limitation of MuZero that it can not be applied to action spaces that cannot be easily enumerated or are not discrete. The method proposed in this paper extends MuZero to the case of arbitrary action spaces.

The proposed method is to sample a subset of actions for the search and the training:

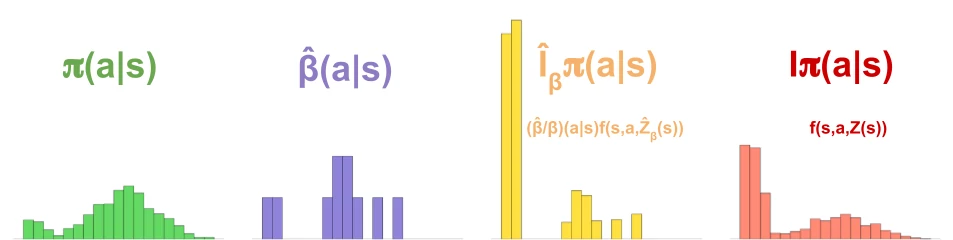
1. Each time a leaf node is expanded, Sampled MuZero samples $K«N$ actions from a distribution $β$, where the paper uses $β=π$
2. MCTS produces an improved distribution \(\hat{I}_β π(a\mid s)\) over the sampled actions. To avoid double counting of probabilities and remain stable, the UCB formula uses \(\frac{\hat{\beta}}{\beta}\pi\) instead of raw $\pi$. The policy is updated on this sampled improvement.