“Hindsight” – An easy yet effective RL Technique HER with Pytorch implementation
Published:
This week, I will share a paper published by OpenAI at NeurIPS 2017. The ideas presented in this paper are quite insightful, and it tackles a complex problem using only simple algorithmic improvements. I gained significant inspiration from this paper. At the end, I will also provide a brief implementation of HER (Hindsight Experience Replay).
Original Paper Information
Title: Hindsight experience replay
Author: Marcin Andrychowicz, Filip Wolski, Alex Ray, Jonas Schneider, Rachel Fong, Peter Welinder, Bob McGrew, Josh Tobin, OpenAI Pieter Abbeel, Wojciech Zaremba
Code: https://github.com/openai/baselines/blob/master/baselines/her/README.md
Background
The combination of reinforcement learning and neural networks has achieved success in various domains involving sequential decision-making, such as Atari games, Go, and robot control tasks.
Typically, in reinforcement learning tasks, a crucial aspect is designing a reward function that reflects the task itself and guides the optimization of the policy. Designing a reward function can be highly complex, which limits the application of reinforcement learning in the real world. It requires not only understanding of the algorithm itself but also substantial domain-specific knowledge. Moreover, in scenarios where it is difficult for us to determine what actions are appropriate, it is challenging to design an appropriate reward function. Therefore, algorithms that can learn policies from rewards that do not require explicit design, such as binary variables indicating task completion, are important for applications.
One capability that humans possess but most model-free reinforcement learning algorithms lack is the ability to learn from “hindsight”. For example, if a basketball shot misses to the right, a reinforcement learning algorithm would conclude that the sequence of actions associated with the shot is unlikely to lead to success. However, an alternative “hindsight” conclusion can be drawn, namely that if the basket were slightly to the right (to the location where the ball landed), the same sequence of actions would result in success.
The paper introduces a technique called Hindsight Experience Replay (HER), which can be combined with any off-policy RL algorithm. HER not only improves sampling efficiency but, more importantly, enables the algorithm to learn policies from binary and sparse rewards. HER incorporates the current state and a target state as inputs during replay, where the core idea is to replay an episode (a complete trajectory) using a different goal than the one the agent was originally trying to achieve.
HER
1. An introducing example
Consider a coin flipping problem with a total of $n$ coins. The configuration of heads or tails for these $n$ coins represents a state, and the state space is denoted as $S={0,1}^n$. The action space is $A={0,1,…,n-1}$, where $i$ denotes flipping the i-th coin. In each episode, an initial state and a target state are uniformly and randomly selected. The RL policy flips these $n$ coins, and if the resulting state differs from the target state, a reward of $-1$ is obtained, i.e., $r_g(s,a)=-[s\neq g]$. Here, $g$ represents the target state.
When $n>40$, reinforcement learning strategies almost always fail because the policy rarely encounters rewards other than $-1$. Relying on random action exploration in such a large state space is impractical. A common approach in reinforcement learning is to design a reward function that guides the policy towards the goal. In this example, $r_g(s,a)=|s-g|^2$ can solve the problem. However, designing a reward function can be challenging, especially when facing more complex problems.
The solution proposed in this paper does not require any domain-specific knowledge. Consider an episode that goes through a sequence of states $s_1, s_2, …, s_T$, and a target $g\neq s_1, s_2, …, s_T$ that has not been achieved. In each step of this episode, a reward of $-1$ is obtained. The method described in the paper involves replacing $g$ with $s_T$ and adding the modified episode to the replay buffer. This approach introduces paths with rewards different from $-1$, making the learning process simpler.
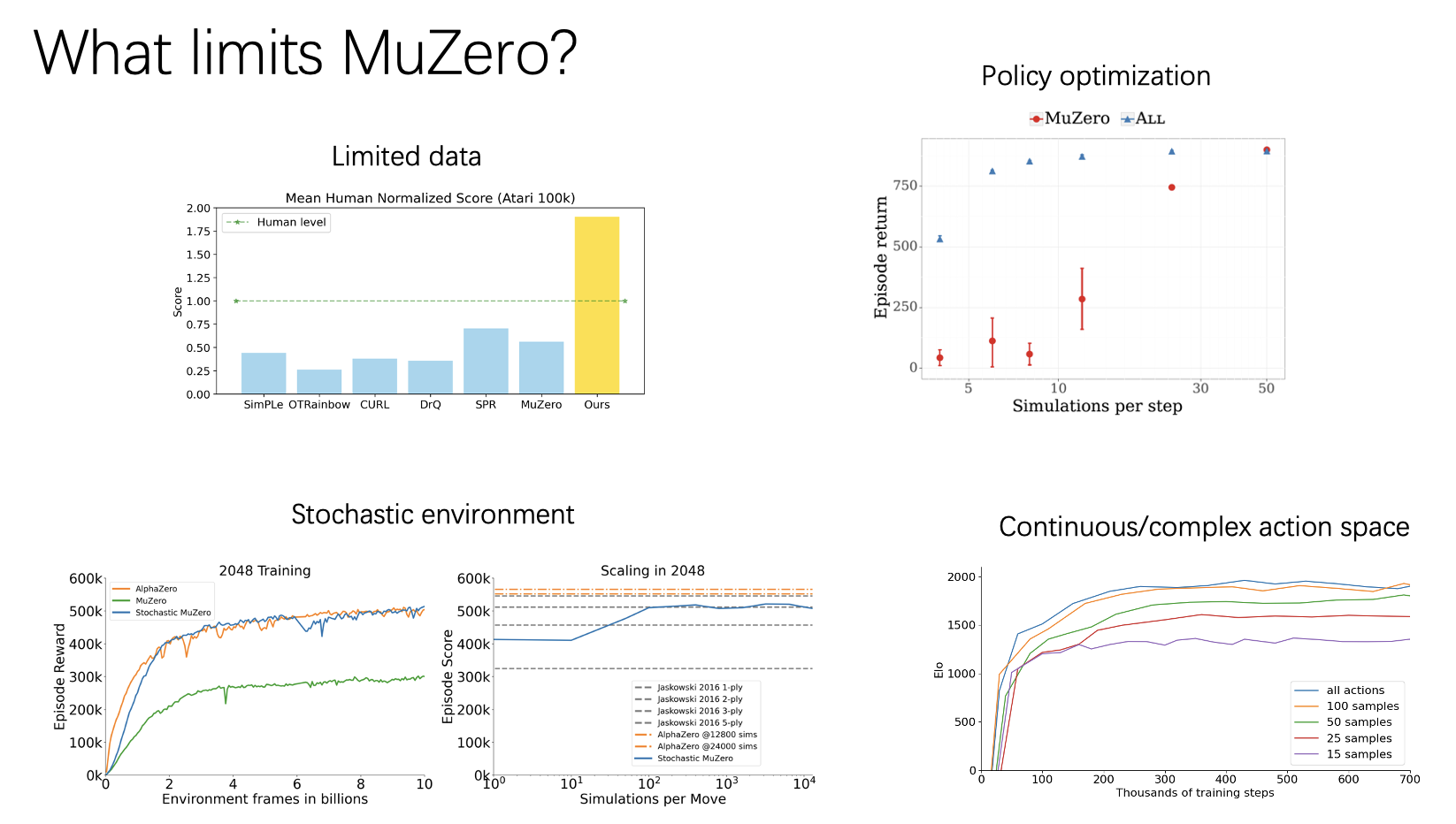
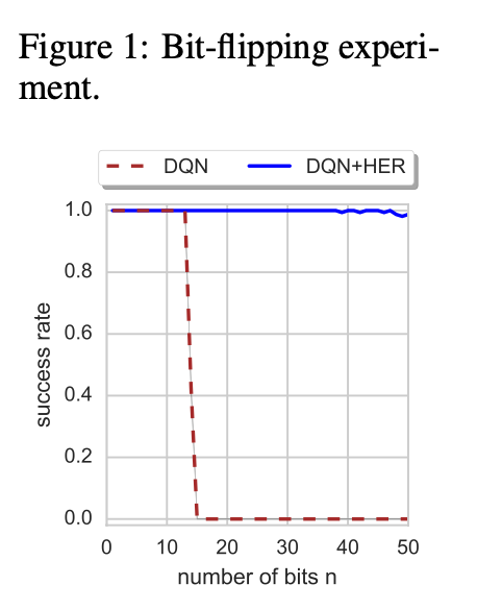
Figure 1 compares the performance of plain DQN and DQN+HER in this environment. DQN without HER can solve problems with at most 13 coins, while DQN+HER can easily handle environments with 50 coins.
2. Multi-goals scenario
The problem scenario of interest involves an agent capable of achieving multiple distinct goals. Let’s assume there exists a set of goals $G$, where each goal $g\in G$ has a corresponding mapping $f_g:S\rightarrow {0,1}$, and the agent’s objective is to reach any state $s$ for which $f_g(s)=1$. For example, a goal could be a specific state itself: $f_g(s)=[s=g]$, or a goal related to a certain property of the state, such as reaching a given x-coordinate in a two-dimensional coordinate system: $f_g((x,y))=[x=g]$.
Furthermore, the paper assumes that given a state $s$, it is straightforward to find a corresponding goal $g$. In other words, there exists a mapping $m:S\rightarrow G$ such that for every $s\in S$, $f_{m(s)}(s)=1$. For instance, in the case of a two-dimensional coordinate system, $m((x, y))=x$.
Using a binary sparse reward function that assigns $-1$ if the goal is not achieved at each time step and 0 if it is achieved does not yield good results during actual training. This is because the reward is too sparse and lacks sufficient information. To address this problem, the original paper proposes the HER algorithm.
3. HER algorithm
The idea behind HER is quite simple: after experiencing a sequence of states $s_1, s_2, …, s_T$, each transition $s_t\rightarrow s_{t+1}$ is saved. These transitions are not only associated with the original goal that generated the sequence but also grouped with a subset of other goals. Different goals only affect the agent’s actions and not the transition probabilities of the entire environment, allowing off-policy algorithms to use different goals during training.
With HER, one task is to define the “subset of other goals.” The simplest approach, $m(s_T)$, involves using only the final state of a single trajectory as a goal.

It’s worth noting that the algorithm of HER differs from a standard off-policy algorithm in a couple of ways. Firstly, the policy’s input is a concatenation of the state vector $s$ and the goal vector $g$. Secondly, the Replay Buffer stores not only the transition information generated through interactions with the environment but also the transition information after replacing the goal with a new goal $g’$. These pieces of information are collectively used for subsequent training.
Experiment
The paper’s experiments can be referenced in the following video:
The organization of the experimental section in the paper is as follows: The first part introduces the reinforcement learning environments used. Subsequently, each section explores the performance differences between DDPG with and without HER, the performance in single-goal scenarios, the impact of designing additional reward functions on performance, the influence of different sampling methods of goals on policy performance, and finally, the deployment of the algorithm on real robots.
1. Environment
The paper used Mujoco and introduced its own environment, which has been made publicly available in the OpenAI Gym

The policy is represented using a MLP with ReLU activation. The training utilizes the DDPG algorithm with the Adam optimizer.
There are three tasks:
Pushing: Pushing a box to a specified position on a table without performing the “grasp” action.
Slide: Sliding a ball to a target position on a smooth table that is outside the arm’s range of motion.
Pick and Place: Picking up a box and placing it at a designated airborne position.
State:
The state is represented by the Mujoco physics engine, including the angles and velocities of each robotic joint, as well as the positions, rotations, angular momentum, and linear momentum of all objects.
Goal:
The goal is the desired position of the object, with a fixed tolerance $\epsilon$. For example, $G=R^3$, where $f_g(s)=[|g-s_{object}|\leq\epsilon]$, and $s_{object}$ represents the position of the object in state $s$. The mapping function is defined as $m(s)=s_{object}$.
Reward:
Except for the section on Reward Design Comparison, the reward is defined as $r(s,a,g)=-[f_g(s’)=0]$, where $s’$ is the resulting state after performing action $a$ in state $s$.
Action:
The action is four-dimensional, with the first three dimensions representing the desired relative position of the robotic gripper in the next time step, and the last dimension representing the desired distance between the two robotic fingers.
2. Can HER improve performance?
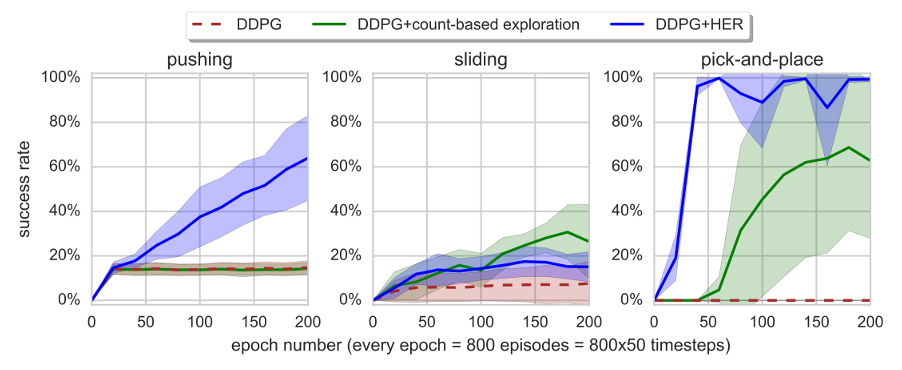
As shown in Figure 4, the performance of DDPG, DDPG with count-based exploration (Strehl and Littman, 2005; Kolter and Ng, 2009; Tang et al., 2016; Bellemare et al., 2016; Ostrovski et al., 2017), and DDPG+HER is compared. The blue line represents HER, which stores the transitions twice - once with the goal that generates interaction data with the environment and once with the goal changed to the state reached at the end of the episode. The red line is the best-performing HER strategy among the different goal selection strategies discussed in Section 5.
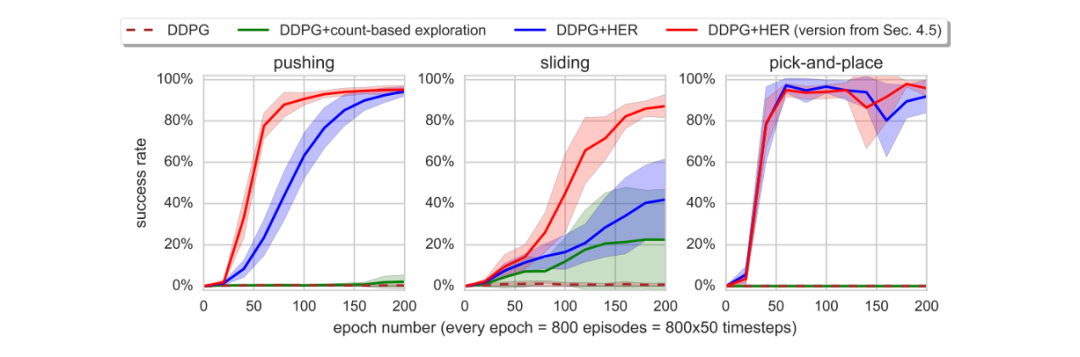
From Figure 4, we can observe that vanilla DDPG fails to learn the policies for all three tasks. DDPG with count-based exploration shows some progress only in the sliding task. However, DDPG+HER excels in solving all three tasks. It can be concluded that HER is crucial for learning policies from sparse and binary rewards.
3. Can HER improve performance when there is only one goal?
In this section’s experiment, the goal for each episode is fixed to be the same (the same target position), repeating the experiment from Section 2. From Figure 5, it can be observed that DDPG+HER outperforms vanilla DDPG. Comparing Figure 4 and Figure 5, it is evident that HER learns faster when there are multiple goals. Therefore, the authors suggest that even if there is only one specific goal of interest, training can still be conducted using a multi-goal approach.
4. How does HER interact with the design of reward functions?
In this part, an attempt is made to design a reward function instead of using the binary sparse reward employed in the previous experiments. A shaped reward is considered: $r(s,a,g)=\lambda |g-s_{object} |^p-|g-s_{object}’ |^p$, where $s’$ represents the state reached after performing action $a$ in state $s$; $\lambda\in{0,1}$ and $p\in{1, 2}$ are hyperparameters.
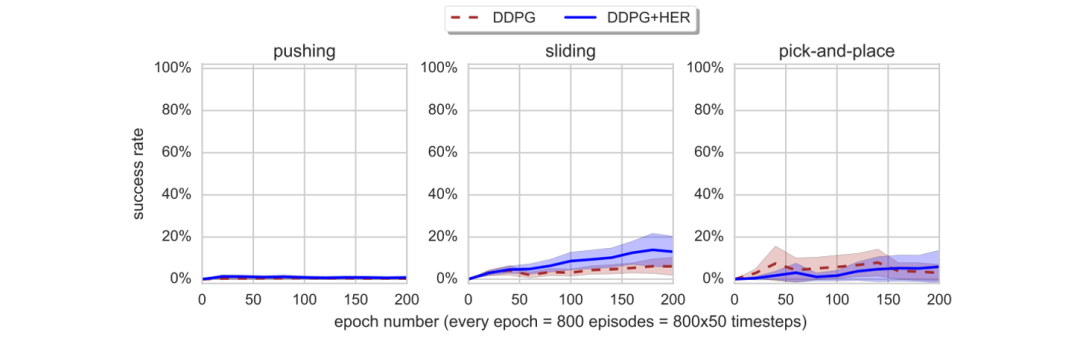
From Figure 6, it can be observed that both vanilla DDPG and DDPG+HER did not learn effective policies. (This is possibly resulted from the fact that when applying reinforcement learning to complex manipulation tasks, it often requires designing reward functions that are much more complex than the ones attempted by the authors.)
The authors believe that the failures stem from two reasons: 1. The optimization objective (shaped reward) differs significantly from the condition for success (whether the final position is within a certain radius of the target). 2. The shaped reward penalizes inappropriate actions, hindering exploration.
While more complex reward designs may potentially address the issue, they require a substantial amount of domain knowledge. This fact reinforces the importance highlighted in the paper of effective learning from binary sparse rewards.
5. How many goals should be chosen and how should they be selected?
In previous experiments, only the final state of an episode was utilized. In this section, additional goal sampling methods are considered. The following methods are taken into account:
- Final: The final state of an episode.
- Random: Randomly select $k$ states encountered throughout the training process.
- Episode: Randomly select $k$ states encountered within a single episode.
- Future: Randomly select $k$ states that appear after the current state within the same episode.
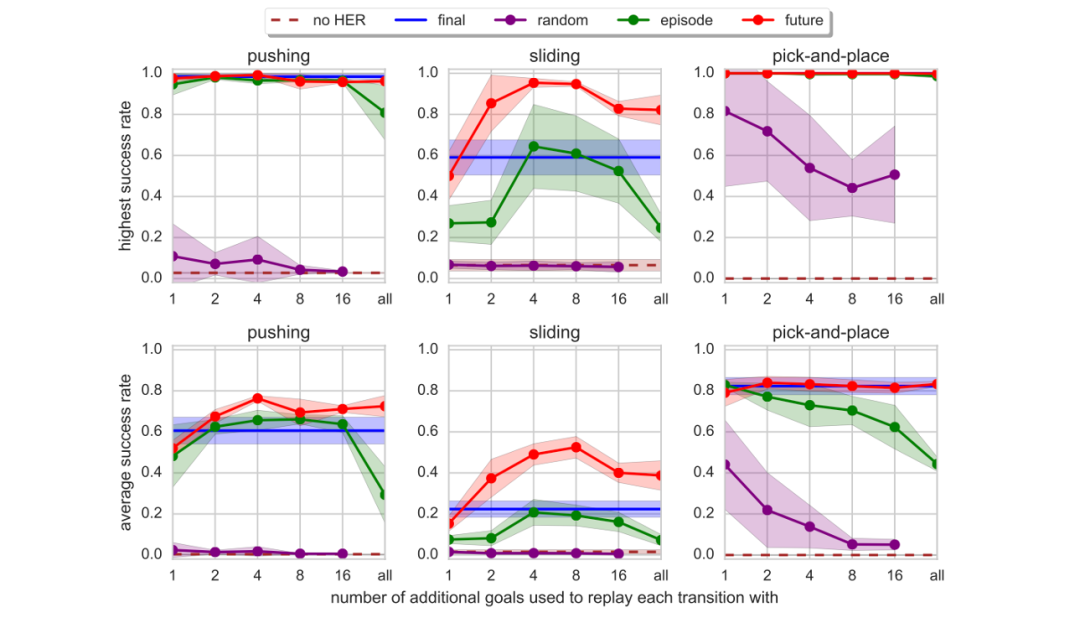
As shown in Figure 7, the top row represents the highest success rate, while the bottom row represents the average success rate. The parameter $k$ controls the ratio between HER data in the Replay Buffer and the data generated by the agent’s interaction with the environment.
It can be observed that for the third task, all goal selection methods except for Random perform remarkably well. Future combined with $k=4$ or $8$ shows the best performance across all tasks and is the only method that performs well in the second task. However, when $k$ exceeds $8$, there is a decline in performance, as the proportion of data generated by the agent’s interaction with the environment becomes relatively low.
6. Deploy on a real robot
Lastly, the authors conducted an experiment where the algorithm (Future, $k=4$) was deployed on a real robot. They added a separately trained CNN layer to recognize camera images. In the initial five trials, the algorithm succeeded twice. However, after introducing noise to the observed data, all five trials were successful.
Conclusion
The contributions of this paper is that:
This paper proposes an innovative method that enables reinforcement learning algorithms to learn complex task policies from simple binary sparse rewards. This approach can be combined with any off-policy algorithm.
Review comments
From NeurIPS review, one can see the questions raised by the reviewers regarding the original paper before its acceptance. Among them, one reasonable suggestion is to explore the combination of HER with a proven effective reward function for evaluating the performance of the combination of HER with reward engineering.
Pytorch implementation
The article is very clear, with interesting ideas and a simple implementation. I personally really like this paper.
Moreover, I attempted to implement HER myself, applying it to the MountainCar-v0 environment in the Gym framework. In this environment, there is a single goal, and a reward of $-1$ is received at each time step until the goal is achieved. Without using HER, the typical approach is to rely on a large number of random actions to discover successful paths or to redesign the reward function. However, with DQN+HER, the policy can be learned relatively quickly, while vanilla DQN requires more time steps and more random exploration.

So first import the necessary libraries:
import os
import gym
from typing import Tuple
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.optim import Adam
import numpy as np
from collections import deque
from itertools import chain
import random
from copy import deepcopy
device = torch.device('cpu' if not torch.cuda.is_available() else 'cuda:0')
seed = 40
random.seed(seed)
np.random.seed(seed)
torch.manual_seed(seed)
os.makedirs(os.path.join('drl', 'DQN'), exist_ok=True)
We define an MLP policy:
class MLPNet(nn.Module):
def __init__(self, input_size, output_size, hidden_size: int = None, num_layers: int = 2):
super().__init__()
self.input_size = input_size
self.hidden_size = hidden_size if hidden_size else input_size
self.output_size = output_size
self.mlp = nn.ModuleList()
self.activation = nn.ReLU()
for i in range(num_layers):
if i == 0:
first = nn.Linear(self.input_size, self.hidden_size)
self.mlp.append(first)
self.mlp.append(self.activation)
else:
hidden = nn.Linear(self.hidden_size, self.hidden_size)
self.mlp.append(hidden)
self.mlp.append(self.activation)
self.classifier = nn.Linear(self.hidden_size, self.output_size)
self.mlp.append(self.classifier)
def forward(self, x):
for module in self.mlp:
x = module(x)
return x
class Net(nn.Module):
def __init__(self, state_dim, action_dim, embedding_dim, is_discrete=True):
super().__init__()
self.embed = nn.Embedding(state_dim, embedding_dim) if is_discrete else nn.Linear(state_dim, embedding_dim)
self.mlp = MLPNet(embedding_dim, action_dim)
def forward(self, x):
x = self.embed(x)
y_pred = self.mlp(x)
return y_pred
And Replay Buffer:
class ReplayBuffer(torch.utils.data.Dataset):
def __init__(self, replay_buffer_capacity: int = 5000, device=None):
super().__init__()
self.type = 'RB'
self.device = device
self.replay_buffer_capacity = replay_buffer_capacity
self.states = deque(maxlen=self.replay_buffer_capacity)
self.actions = deque(maxlen=self.replay_buffer_capacity)
self.rewards = deque(maxlen=self.replay_buffer_capacity)
self.next_states = deque(maxlen=self.replay_buffer_capacity)
self.dones = deque(maxlen=self.replay_buffer_capacity)
def __len__(self):
return len(self.states)
def __getitem__(self, index):
return (
self.states[index], self.actions[index], self.rewards[index], self.next_states[index], self.dones[index]
)
def append(self, trans: Tuple):
'''
trans: (state, action, reward, next_state, done)
follows OpenAI gym
'''
self.states.append(trans[0])
self.actions.append(trans[1])
self.rewards.append(trans[2])
self.next_states.append(trans[3])
self.dones.append(trans[4])
And HER:
class HER(ReplayBuffer):
def __init__(self, reward_func, m_func, sample_strategy = 'final', k_goals: int = 1, replay_buffer_capacity: int = 5000, device=None):
super().__init__(replay_buffer_capacity=replay_buffer_capacity, device=device)
self.reward_func = reward_func
self.m_func = m_func
if sample_strategy not in ['final', 'random']:
raise ValueError(f"{sample_strategy} is not in ['final', 'random']")
self.sample_strategy = sample_strategy
self.type = 'HER'
self.k_goals = k_goals
def append(self, trans: Tuple, goal: np.array):
'''
goal is a vector
'''
s, a, r, ns, d = trans
goal = np.array(goal)
size = self._goal_size(goal)
s = np.hstack([s, goal])
r = self.reward_func(s[:-size], a, s[-size:])
ns = np.hstack([ns, goal])
# print(f'append:{(s, a, r, ns, d)}')
super().append((s, a, r, ns, d))
def hindsight(self, ep_len: int):
'''
At the end of episode, append hindsight
'''
# print(f'ep_len: {ep_len}')
if self.sample_strategy == 'final':
s, a, r, ns, d = deepcopy(self[-1])
g = self.m_func(s)
R_, tail = 0, 0
for _ in range(self.k_goals):
R_tmp, tail = self.hindsight_append(ep_len, g, tail)
R_ += R_tmp
R_ /= self.k_goals
if self.sample_strategy == 'random':
R_, tail = 0, 0
for _ in range(self.k_goals):
s, a, r, ns, d = deepcopy(random.choice(self))
g = self.m_func(s)
R_, tail = self.hindsight_append(ep_len, g, tail)
R_ /= self.k_goals
return R_
def hindsight_append(self, ep_len: int, g: np.array, tail=0):
g = np.array(g)
size = self._goal_size(g)
R_ = 0
for i in range(ep_len):
s, a, r, ns, d = deepcopy(self[-(i + 1 + tail)])
s[-size:] = g
ns[-size:] = g
r = self.reward_func(s[:-size], a, s[-size:])
# print(f'hindsight_append:{(s, a, r, ns, d)}')
super().append((s, a, r, ns, d))
tail += 1
R_ += r
return R_, tail
def _goal_size(self, g: np.array):
if not g.shape: # np.array(1).shape -> ()
size = 1
else:
size = g.shape[0] # np.array([1]).shape -> (1,)
return size
DQN:
class BaseAgent(nn.Module):
def __init__(self):
super().__init__()
self.name = 'base'
def _preprocess_state(self,state):
if type(state) != torch.Tensor:
state = torch.tensor(state, dtype=torch.float, device=device)
return state
def save(self, path):
pass
def load(self, path):
pass
class DQN(BaseAgent):
def __init__(self, state_size, action_size, goal_size: int = None,
replay_buffer = None,
gamma: float = 0.9,
epsilon: float = 0.8,
tau: float = 500,
cost: torch.nn.modules.loss = nn.MSELoss(reduction='mean'),
lr: float = 0.0001,
gradient_steps: int = 50,
**kwargs
):
super().__init__()
self.name = 'DQN'
self.state_size = state_size
self.action_size = action_size
self.replay_buffer = replay_buffer if replay_buffer is not None else ReplayBuffer(replay_buffer_capacity=20000)
self.is_her = self.replay_buffer.type == 'HER'
self.gamma = gamma
self.epsilon = epsilon
assert 0 < epsilon < 1
self.tau = tau
self.cost = cost
if not self.is_her:
self.main_network = Net(state_size, action_size, 16, is_discrete=False)
self.target_network = Net(state_size, action_size, 16, is_discrete=False)
if self.is_her:
assert goal_size is not None
self.goal_size = goal_size
self.main_network = Net(state_size + self.goal_size, action_size, 16, is_discrete=False)
self.target_network = Net(state_size + self.goal_size, action_size, 16, is_discrete=False)
self.optimizer = Adam(self.main_network.parameters(), lr=lr)
self.gradient_steps = gradient_steps
def store_transition(self, *args):
'''
s, a, r, ns, d, (g if her)
'''
if not self.is_her:
self.replay_buffer.append(args)
if self.is_her:
trans_g = [*args]
trans, g = trans_g[:-1], trans_g[-1]
self.replay_buffer.append(trans, g)
def epsilon_greedy(self, state, goal=None):
if random.uniform(0, 1) < self.epsilon:
action = np.random.randint(self.action_size)
else:
if not self.is_her:
action = np.argmax(
self.main_network(self._preprocess_state(state)).tolist()
)
else:
assert goal is not None
action = np.argmax(
self.main_network(self._preprocess_state(np.hstack([state, goal]))).tolist()
)
return action
def best_q_action(self, state, goal=None):
if not self.is_her:
action = np.argmax(
self.main_network(self._preprocess_state(state)).detach().cpu().numpy()
)
else:
goal = np.array(goal)
s_g = np.hstack([state, goal])
action = np.argmax(
self.main_network(self._preprocess_state(s_g)).detach().cpu().numpy()
)
return action
def train(self, batch_size):
if len(self.replay_buffer) < batch_size:
return
loader = torch.utils.data.DataLoader(self.replay_buffer, batch_size=batch_size, shuffle=True)
# minibatch = random.sample(self.replay_buffer, batch_size)
for _ in range(self.gradient_steps):
s, a, r, ns, done = next(iter(loader))
s = s.to(dtype=torch.float32)
ns = ns.to(dtype=torch.float32)
# print(done)
max_tensor, max_idx = self.target_network(ns).max(dim=1)
target_Q = (r + (1 - done.long()) * self.gamma * max_tensor).to(dtype=torch.float32)
Q_values = self.main_network(s)
Q_targets = Q_values.clone()
Q_targets[torch.arange(Q_targets.size(0)), a] = target_Q
loss = self.cost(Q_values, target=Q_targets)
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
def update_target_network(self):
self.target_network.load_state_dict(self.main_network.state_dict())
def _preprocess_state(self,state):
if type(state) != torch.Tensor:
state = torch.tensor(state, dtype=torch.float)
return state
def save(self, path):
torch.save(
{'main_network_sd': self.main_network.state_dict()}, path)
def load(self, path):
self.main_network.load_state_dict(torch.load(path)['main_network_sd'])
self.target_network.load_state_dict(self.main_network.state_dict())
The training and evaluating functions:
def train(agent: DQN, env, num_episodes: int = 500, num_timesteps: int = 300, batch_size: int = 16, update_every: int = 50, require_render: bool = True, is_her: bool = False, require_epsilon_explore: bool = True, save_path=None, **kwargs):
save_path = save_path if save_path is not None else os.path.join('drl', agent.name)
done = False
time_step = 0
cur_best = -np.inf
Return_list = []
if agent.is_her:
is_her = True
if is_her:
try:
goal = kwargs['goal']
except KeyError:
raise ValueError('No env goal has been provided.')
if agent.name == 'DQN':
steps = 0
if require_epsilon_explore:
epsilon_decay = agent.epsilon - 0.2
for i in range(num_episodes):
Return = 0
state = env.reset()
# Cart-Pole
# if np.mean(Return_list[-10:]) == 200:
# break
for t in range(num_timesteps):
steps += 1
if require_render:
env.render()
time_step += 1
if time_step % agent.tau == 0:
agent.update_target_network()
if not is_her:
action = agent.epsilon_greedy(state)
else:
action = agent.epsilon_greedy(state, goal)
next_state, reward, done, info = env.step(action)
if not is_her:
agent.store_transition(state, action, reward, next_state, done)
else:
agent.store_transition(state ,action, reward, next_state, done, goal)
state = next_state
Return += reward
if done:
if is_her:
Return_ = agent.replay_buffer.hindsight(t + 1)
print(f'Episode:{i}, Return_her:{Return_}')
Return_list.append(Return)
print(f'Episode:{i}, Return:{Return}')
if Return >= cur_best:
agent.save(save_path)
cur_best = Return
break
if steps % update_every == 0:
agent.train(batch_size)
if require_epsilon_explore:
agent.epsilon -= (1/num_episodes) * epsilon_decay # more exploitation
env.close()
return Return_list
def evaluate(agent, env, num_timesteps: int = 200, require_render=True, **kwargs):
done = False
Return = 0
state = env.reset()
if agent.is_her:
is_her = True
else:
is_her = False
if is_her:
try:
goal = kwargs['goal']
except KeyError:
raise ValueError('No env goal has been provided.')
if agent.name == 'DQN':
# best action
for t in range(num_timesteps):
if require_render:
env.render()
if not is_her:
action = agent.best_q_action(state)
else:
action = agent.best_q_action(state, goal)
next_state, reward, done, info = env.step(action)
state = next_state
Return += reward
if done:
print(f'Return:{Return}')
break
env.close()
return Return
Define the reward and $m$ of MountainCar-v0:
def reward_func_MountainCar(s, a, goal):
'''
In the original code:
done = bool(position >= self.goal_position and velocity >= self.goal_velocity)
'''
if s[0] >= goal[0]:
return 0
else:
return -1
def m_MountainCar(s):
'''
m: S -> G
for MountainCar environment, s[0] is the position, s[1] is the velocity. The goal is s[0] == 0.5 and s[1] == 0
'''
g = np.array([s[0], s[1]])
return g
Run experiment:
env_name = 'MountainCar-v0'
env = gym.make(env_name)
her = HER(reward_func=reward_func_MountainCar, m_func=m_MountainCar, sample_strategy='final', replay_buffer_capacity=20000, k_goals=2)
dqn_her = DQN(state_size=env.observation_space.shape[0], action_size=env.action_space.n, goal_size=2, replay_buffer=her, gradient_steps=10, lr=.001)
dqn = DQN(state_size=env.observation_space.shape[0], action_size=env.action_space.n, gradient_steps=10, lr=.001)
save_path = os.path.join('drl', dqn_her.name, env_name)
return_path_her = train(dqn_her, env, num_episodes=200, save_path=save_path, num_timesteps=200, update_every=10, batch_size=32, goal=np.array([.5, 0]))
num_tests = 10
Rs = 0
for i in range(num_tests):
Return = evaluate(dqn_her, env, num_timesteps=200, require_render=True, goal=np.array([0.5, 0]))
Rs += Return
print(Rs / num_tests)
# In comparison
return_path_dqn = train(dqn, env, num_episodes=200, save_path=save_path, num_timesteps=200, update_every=10, batch_size=32)
num_tests = 10
Rs = 0
for i in range(num_tests):
Return = evaluate(dqn, env, num_timesteps=200, require_render=True)
Rs += Return
print(Rs / num_tests)
Check my post on Discovery Lab: 【每周一读】“事后诸葛亮”——一种简单有效的强化学习技术HER(文末附Pytorch代码)