Image you were a new student in Columbia and were asked to go to Mudd. How would you find the way? Probably as most people do, you will need a map. And if you have a map with your location within it, it’s even better. It is kind of similar for the robotic tasks, where autonomous operations requires the agent to have access to a consistent model of the surrounding environment. To have a map with one’s location is about localization and mapping, which are correlated and dependent of one another. Previous works focus on incrementally building the map of the environment while at the same time locating the robot within it, which is referred to as SLAM. Moreover, different strategies can be applied to guide the robot to explore the unknown environment, which are gaining increasing attention. The rapid advances in deep learning and more RL friendly simulators have stimulated the deep reinforcement learning (DRL) research interest in active SLAM. Several works, also demonstrate the success of introducing DRL into embodied AI tasks.

However, the current DRL for active SLAM has their focus on model-free algorithms, which is lack of planning abilities and is less efficient compared to model-based ones. And the recent progress of MuZero has tackled the difficulties that other model-based algorithms have when solving Atari Games, to outperform the state-of-the-art result from model-free algorithm and establish a new one. Despite the growing interest in the mcts-based algorithms, implementing these algorithms and adapting them to specific tasks remains a challenging endeavor.

In this project, a model-based method Neural Tree Search is proposed for active SLAM, which follows the search process as MuZero, while introduces a SLAM module, which decodes the predicted map from the hidden state for path planning. A corresponding loss function is proposed to train the NTS model.

Method

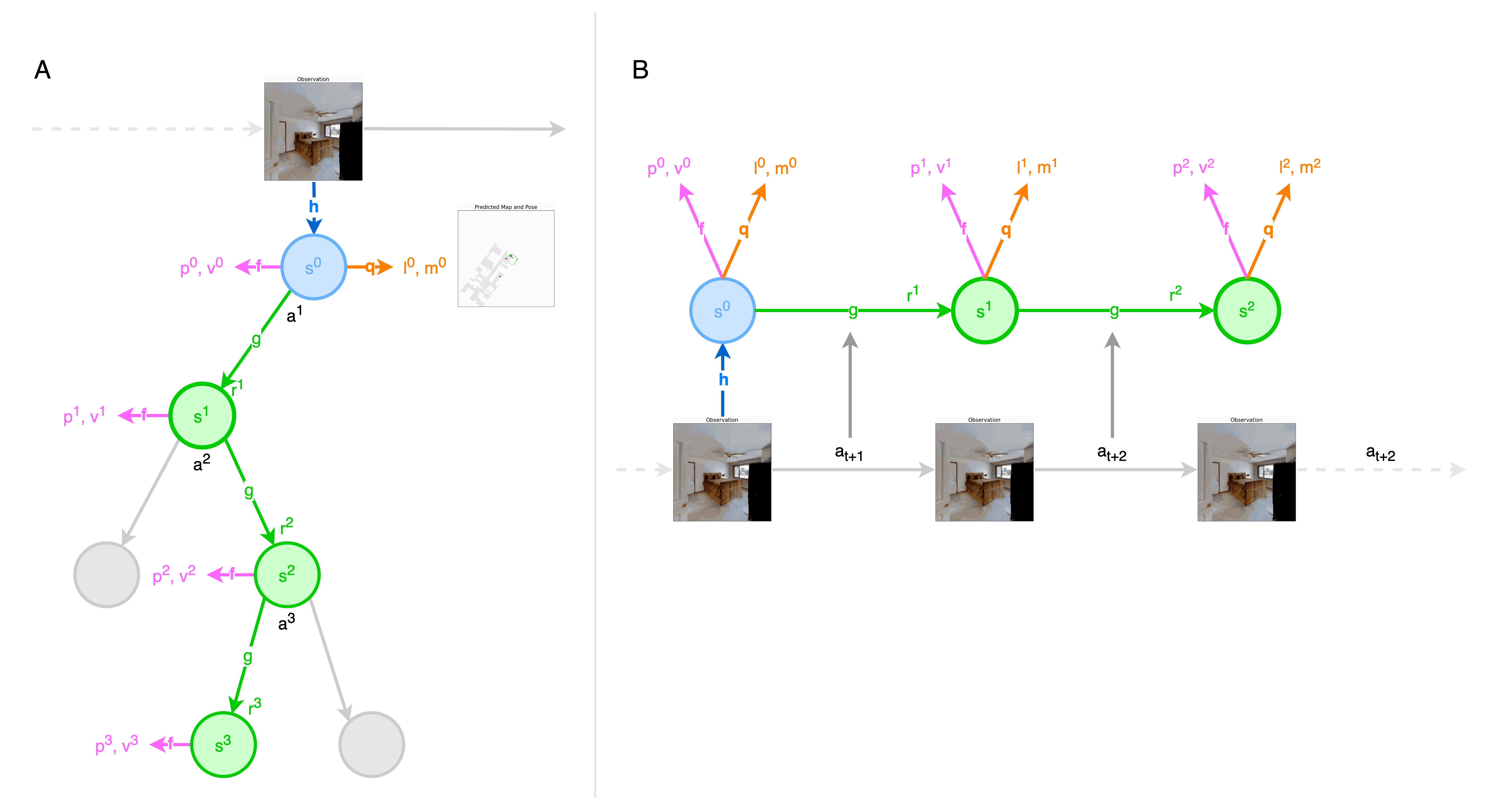
(A) shows how NTS uses its model to plan. The model consists of four connected components for representation, dynamics, prediction and SLAM. The initial hidden state $s^0$ is the output of representation module $h$, whose input is the raw observations, for instance, an RGB image of the room to be explored. For each hidden state $s^k$, the policy $p^k$ and value $v^k$ are predicted by the prediction module $f$ and the predicted map $m^k$ and predicted location $l^k$( in the predicted map) are gathered from SLAM module. Then, Given a hidden state $s^{k-1}$ and a candidate action $a^k$, the dynamics module $g$ produces an immediate reward $r^k$ and a new hidden state $s^k$.
(B) shows how NTS is trained. For one sub trajectory sampled from replay buffer, the representation module $h$ generates the initial hidden state $s^0$ from the past observations $o_t$ from the first timestep of the sampled trajectory. The model is subsequently unrolled recurrently for K steps. At each step k, five pairs of quantities are predicted to calculate the loss, namely the predicted policy $p^k$ with the action probability from the root node $\pi_{t+k}$, the preidcted value $v^k$ with the n-step bootstrapping value $z_{t+k}$, the predicted reward $r^k$ with the actual reward received $u_{t+k}$, the predicted map $m^k$ with the ground truth map $d_{t+k}$, the predicted location $l^k$ with the actual location $e_{t+k}$. Then the dynamics module $g$ receives as input the hidden state $s^{k-1}$ from the previous step and the real action $a_{t+k}$, to generate the next hidden state $s^{k}$. Four modules are jointly trained.

To train the extended model end-to-end, NTS combines the MuZero loss with SLAM loss: \(l_t(\theta)=\sum_{k=0}^Kl^r(u_{t+k}, r_t^k)+l^v(z_{t+k},v_t^k)+l^p(\pi_{t+k},p_t^k)\\ +l^{map}(d_{t+k}, m_{t}^k)+l^{pose}(e_{t+k}, l_t^k)+c||\theta||^2\) where $l^r, l^v, l^p, l^{map}, l^{pose}$ are loss functions for reward, value, policy, map, location, respectively.

Result

Comparision experiments on Gibson exploration task against Neural SLAM are proposed.

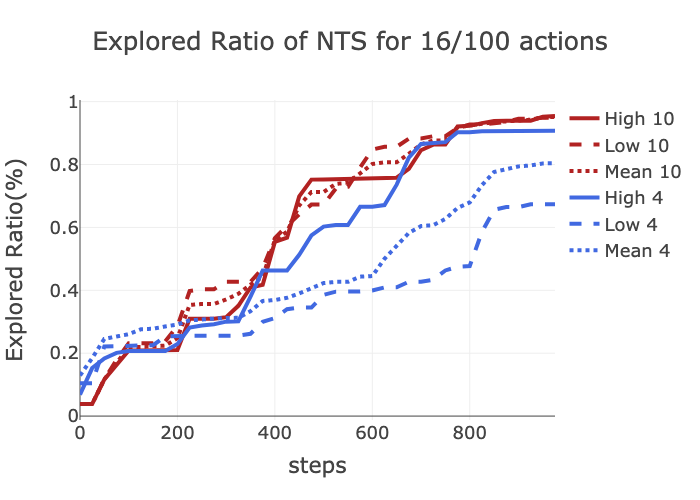
As displayed, NTS 10 realizes competitive performance to Neural SLAM with 30 episodes, the latter requires over 70 episodes and vectorized environment, which demonstrates the efficiency of NTS and the gain from planning. However, NTS 4 is not comparable to NTS 10 and Neural SLAM, and has higher variance. One possible reason is that the robot is blocked by some obstacle and unable to make small adjustment. For example, entering a door.

For more details, please see my report and code: Report, Code